Robust Attribution Regularization
Recent work on training neural networks to have robust attributions, to improve their trustworthiness and resilience to adversarial attacks.
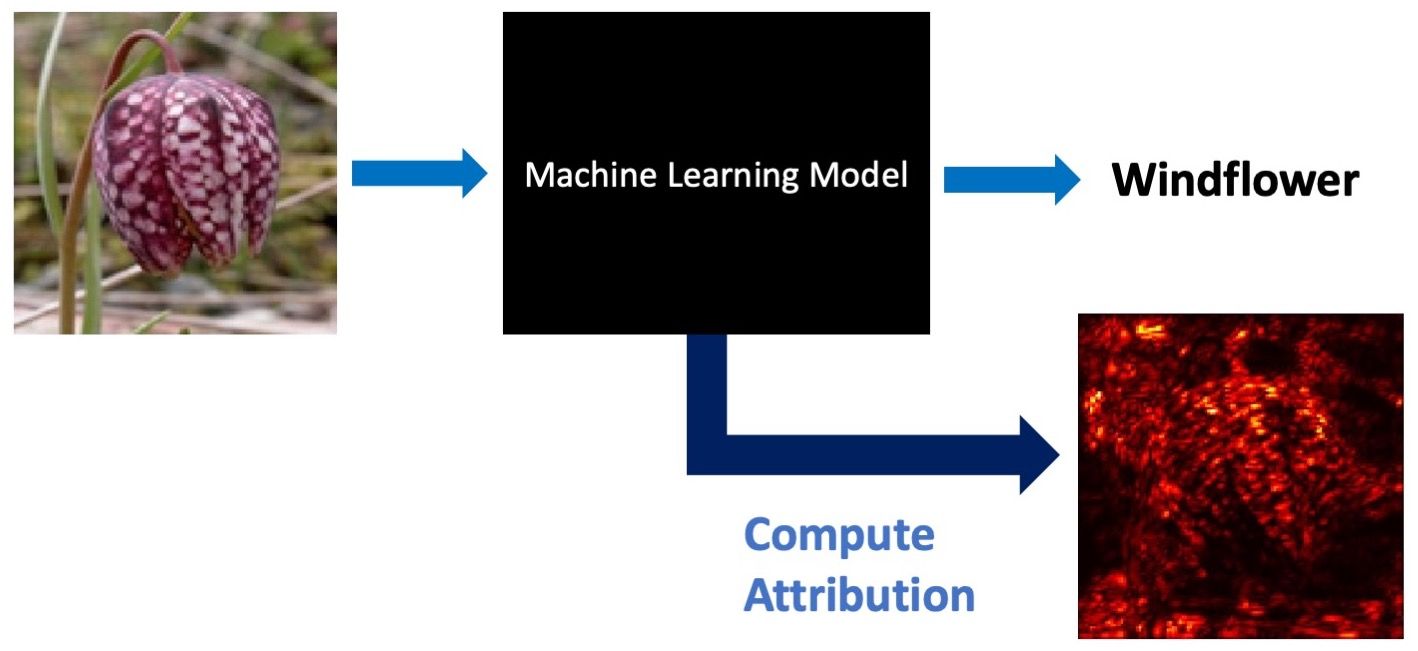
When a human explains how they identify a certain object in an image, they may attribute their identification to certain parts of the image. If this attribution changes substantially when a very similar image is presented, it is an indication that their understanding of the concept is somehow not solid, or robust. Deep Learning models often exhibit such brittleness of attribution, and this makes them both difficult to trust and vulnerable to adversarial examples. This raises a natural question: can we train deep learning models to have robust attributions, and hence alleviate these issues? In this post, Jiefeng Chen and Xi Wu describe intriguing new results from their recent NeurIPS 2019 paper[1] (co-authored with Vaibhav Rastogi, Yingyu Liang and Somesh Jha) on robustifying model attribution and the various benefits of doing so.
-- Prasad Chalasani
Motivation
Fundamental to human perception is the concept of attribution (according to Merriam-Webster, "attribution" means "to explain (something) by indicating a cause"). Even at a very young age, humans can already attribute (and oftentimes surprisingly well). For example, when we show a picture of animals to a 3-year old kid and ask "Do you see a dog?" -- "Yes!" he or she answers; "So what makes you think so?" -- he or she will point to the part of the picture that accounts for a dog -- that's attribution. Perhaps more importantly, robust attribution plays a fundamental role for humans to check whether one has learned the concept correctly. For example, if for a very similar image the same conversation leads the kid to point to a birdie and say "that's the dog!" then this indicates that he or she has not learned what a dog really looks like.
Interestingly, while attribution plays a critical role in human learning, it has (until very recently) received very little attention in machine learning, and in particular deep learning, even though the holy grail of machine learning is to be able to learn to generalize -- or intuitively to learn the "ground truth causality". This is not surprising, however -- if we have learned to be able to predict accurately on unseen instances -- we must have learned the true underlying concept, so it is natural to wonder why one should bother with attribution. After all, deep learning has achieved unprecedented success in domains such as Computer Vision, Natural Language Processing, Game Playing, etc., why should we bother about their attributions?
This lack of attention to attribution has been changing over the past few years, with the discovery of adversarial examples[2][3]. The Achilles' heel of the above "no need for attribution due to high prediction accuracy" argument is the existence of spurious correlations. Classical machine learning theory assumes i.i.d. samples and a "low complexity" hypothesis class to start with, in order to eventually be able to generalize. Unfortunately, neither of these two assumptions hold for deep learning: (1) Samples may be taken with inherent bias that we are not aware of (for example, pictures of cows may all have a green background), and (2) Deep models have huge “capacity” (i.e. large number of trainable parameters). The end result is that deep learning models can easily absorb spurious correlations and can superficially achieve high prediction accuracy, but can easily break down in slightly different but still very natural contexts. We list two examples here:
- Brittle predictions: Traditional adversarial examples. For example, adding small noise to an image of a stop sign may cause the deep learning model to misclassify it as "Max Speed 100", which points to the danger of blindly deploying (even highly accurate) models in critical applications such as self-driving cars.

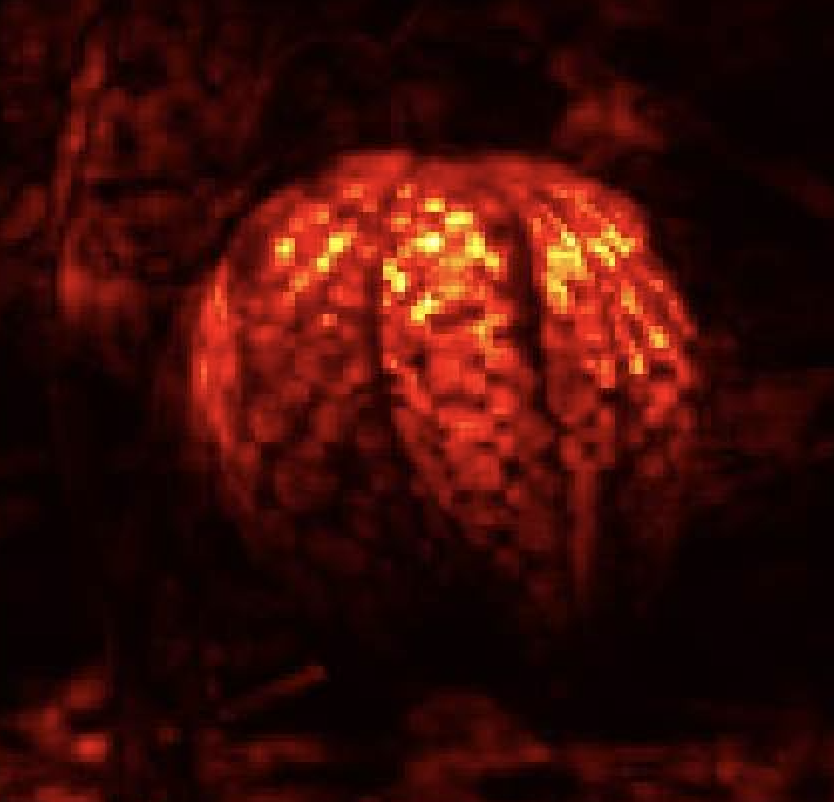
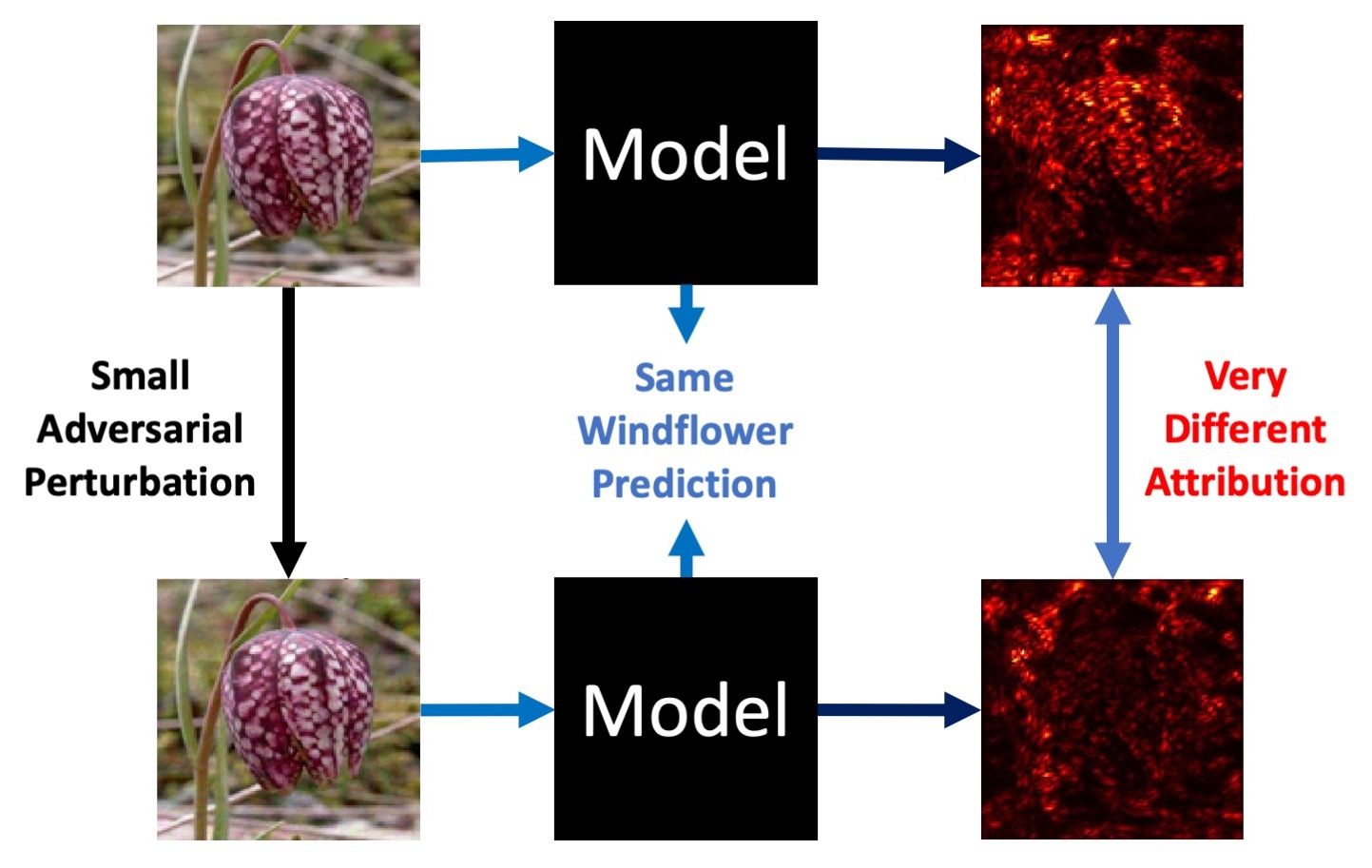
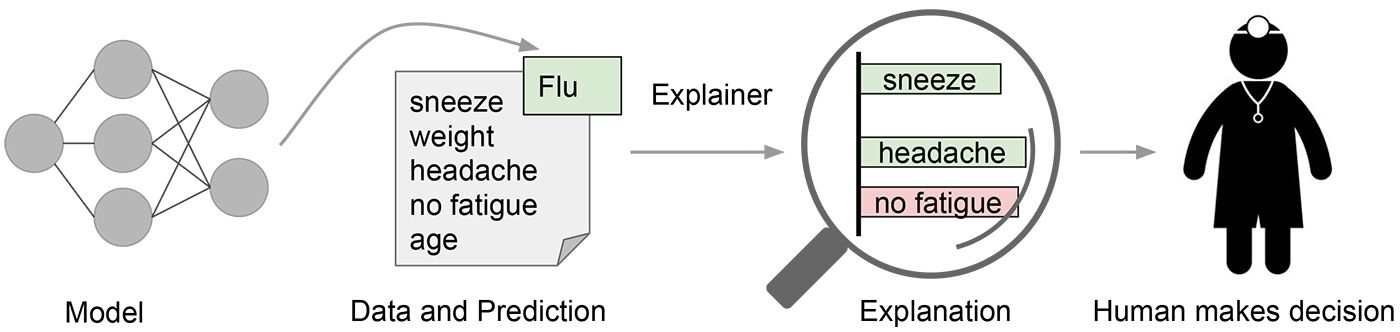
- Brittle attributions: How can doctors trust deep models? As Ghorbani, Abid, and Zou [4] convincingly demonstrated, for existing deep models, one can generate minimal input perturbations that substantially change model attributions, while keeping their (correct) predictions intact (see Fig. 3). Thus, images that look very similar to a human may have very different attributions, a phenomenon that can seriously erode trust in such models. For example, when a doctor uses a deep model as a diagnostic tool, they usually want to know which features cause the model to detect a certain disease. If the attributions are brittle, doctors will find it difficult to trust the model.
We believe that to address brittle predictions and attributions (and other artifacts arising from spurious correlations) in Machine Learning, the key is to enforce robustness of attributions.
Robust Attribution Regularization: A Quick Tour
In our recent work which will appear in NeurIPS 2019, we introduce Robust Attribution Regularization (RAR)[1:1]. RAR aims to regularize the training so the resulting model will have robust attributions that are not substantially changed under minimal input perturbations. To compute attributions of models, we use Integrated Gradients (IG), which is a principled method that has been covered in detail in several posts on this blog (The Axioms of Attribution and Path Methods for Feature Attribution). Note that attributions computed by IG, much like attributions given by the kid in the above example, offer clues of the model's (or equivalently the kid's) thinking.
At a high level, the RAR formulation is very simple and intuitive. If we let $\Delta(\mathbf{x})$ denote the set of allowed (predefined) perturbations $\mathbf{x’}$ of an input instance $x$, the RAR objective discourages (via an additive regularization term) large differences between the attribution for $\mathbf{x}$ and the attribution for $\mathbf{x’}$ (in the worst case sense over perturbations $\mathbf{x’} \in \Delta(\mathbf{x})$). In our paper, attribution is captured by Integrated Gradients applied to the loss function in the supervised learning setting (other formulations are possible and we leave these for future work). Thus we augment the traditional machine-learning objective function with an additional “attribution-regularizer” term, yielding the objective:
\begin{align*} & \min_\theta \mathbb{E}_{(\mathbf{x}, y)\sim \mathcal{D}}[\ell(\mathbf{x},y;\theta)+\lambda*RAR] \\ & where\ RAR = \max_{\mathbf{x'}\in \Delta(\mathbf{x})} s(IG(\mathbf{x},\mathbf{x'})) \end{align*}
Here, $s$ is the size function (which we elaborate on below), $\mathcal{D}$ is the data distribution, $\mathbf{x}$ is the input, $y$ is the label, $\theta$ denotes the vector of model parameters, $\ell$ is the loss function, $\lambda$ is the regularization parameter, $\mathbf{x'}$ is the perturbed input, $\Delta(\mathbf{x})$ is the set of allowed perturbations, and $IG(\mathbf{x}, \mathbf{x’})$ denotes the Integrated Gradients vector for $\mathbf{x}$ with $\mathbf{x’}$ as the baseline (see our previous post for the precise definition of IG).
In simple terms, the RAR objective captures our desire to simultaneously achieve two goals:
- A good prediction accuracy as captured by the original loss term, and
- Attribution must be stable w.r.t. the perturbations
Interestingly, while at first glance this objective function seems unrelated to adversarial training, our theoretical analysis reveals that RAR offers a rich and principled generalization to it. In fact, if one uses $\sum_{i} a_i$ as the size function $s(a)$, and define the permissible perturbation-set $\Delta(\mathbf{x})$ as those where no component is perturbed by more than some $\varepsilon > 0$ (these are referred to as $l_\infty$-norm-bounded perturbations), then via a straightforward calculation using the Completeness Axiom of IG, one can show that the RAR objective degenerates to the adversarial training objective (for robust predictions) of Madry et al.[5]! Furthermore, our paper shows that not only adversarial training, but several objectives (including ones in different robust optimization models) could be viewed as special weak cases of "robust attributions". This gives rise to our first major point about the RAR theory:
Robust attribution regularization gives principled generalizations of previous objectives designed for robust predictions, in both uncertainty set model and distributional robustness model. Moreover, for 1-layer neural networks, RAR naturally degenerates to max-margin training.
Our empirical evaluation of RAR also gives encouraging results and interesting observations. We perform experiments on four classic datasets: MNIST[6], Fashion-MNIST[7], GTSRB[8], and Flower[9]. To evaluate attribution robustness, we use attribution attacks proposed by Ghorbani et al.[4:1] to perturb the inputs (thus causing changes in attributions) while keeping predictions intact, and use Top-K intersection and Kendall’s Correlation as metrics to measure rank correlations between original and perturbed saliency maps (higher values of these metrics indicate more robust attributions). Our main findings can be summarized as follows:
- Compared with naturally trained models, RAR only results in a very small drop in test accuracy. In fact, we believe that such a drop is actually "the right thing to do" because for RAR it is harder to exploit spurious correlations;
- On the other hand, our method gives significantly better attribution robustness, as measured by correlation analyses;
- Our models yield comparable prediction robustness (sometimes even better), compared with adversarially trained models (for robust prediction), while consistently improving attribution robustness;
- Intriguingly, RAR leads to much more human aligned attribution.
To make the discussion more concrete, let us consider the following figure as an example:
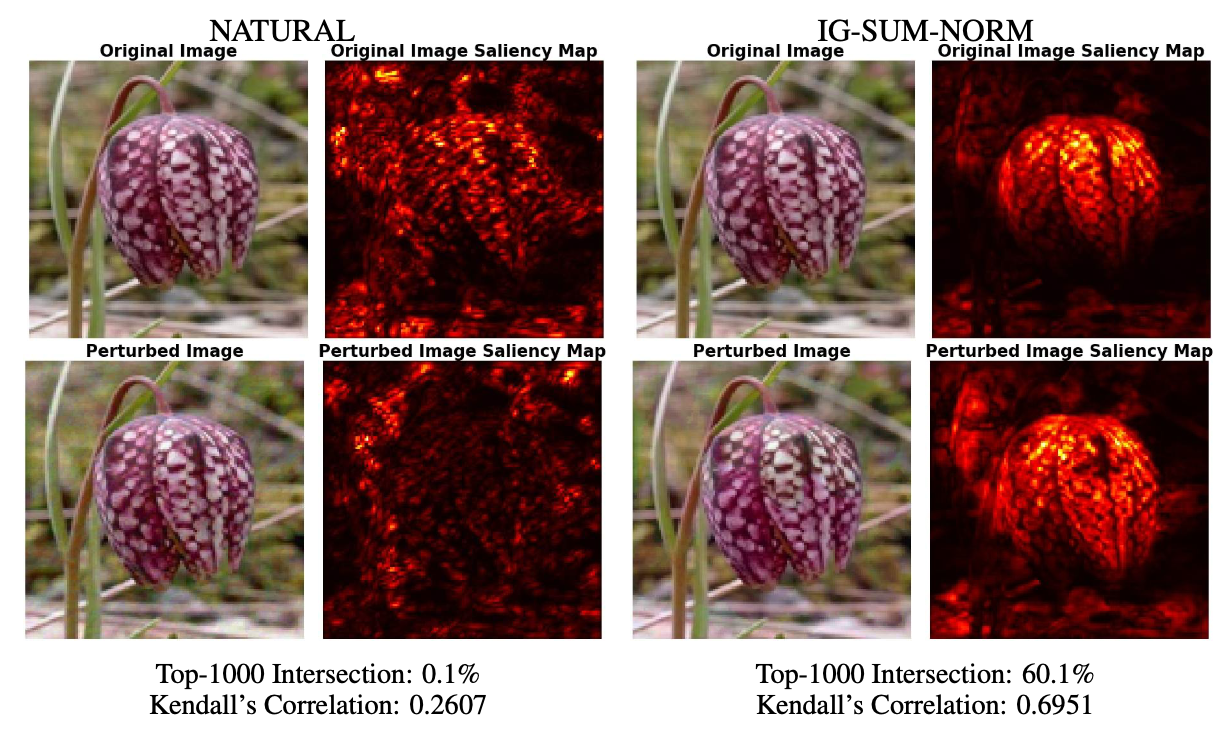
Here NATURAL denotes the naturally trained model, and IG-SUM-NORM is the model trained using our robust attribution method (here we set the size function $s(a)=\sum_{i} a_i+||a||_1$ ). For all images, the models give correct prediction – Windflower. However, the saliency maps, computed via IG, show that attributions of the naturally trained model are very fragile: this is both visually apparent and also reflected in the low intersection and correlation scores. By contrast, the model trained using our RAR method is much more robust in its attributions. It is intriguing to note that the attributions of the RAR-based model are more human-aligned: they precisely highlight the flower!
Conclusion
RAR only scratches the surface of leveraging attributions in deep learning. Our results are encouraging and they hint strongly that robust attributions can help protect models from spurious correlations: intuitively, one cannot reliably attribute to spurious correlations. We hope this post inspires research efforts to further explore this potential connection.
Jiefeng Chen, Xi Wu, Vaibhav Rastogi, Yingyu Liang, and Somesh Jha. "Robust Attribution Regularization." arXiv preprint arXiv:1905.09957 (2019). https://arxiv.org/abs/1905.09957 ↩︎ ↩︎
Goodfellow, Ian J., Jonathon Shlens, and Christian Szegedy. "Explaining and harnessing adversarial examples." arXiv preprint arXiv:1412.6572 (2014). ↩︎
Zico Kolter and Aleksander Madry. "Adversarial robustness – theory and practice." https://adversarial-ml-tutorial.org/. ↩︎
Ghorbani, Amirata, Abubakar Abid, and James Zou. "Interpretation of neural networks is fragile." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 33. 2019. ↩︎ ↩︎
Madry, Aleksander, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. "Towards deep learning models resistant to adversarial attacks." arXiv preprint arXiv:1706.06083 (2017). ↩︎
Yann LeCun, Corinna Cortes, and Christopher J.C. Burges. "The mnist database of handwritten digits", 1998. http://yann.lecun.com/exdb/mnist/. ↩︎
Han Xiao, Kashif Rasul, and Roland Vollgraf. "Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms." arXiv preprint arXiv:1708.07747, 2017. ↩︎
Johannes Stallkamp, Marc Schlipsing, Jan Salmen, and Christian Igel. "Man vs. computer: Benchmarking machine learning algorithms for traffic sign recognition." Neural networks, 32:323–332, 2012. ↩︎
M-E Nilsback and Andrew Zisserman. "A visual vocabulary for flower classification." In 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), volume 2, pages 1447–1454. IEEE, 2006. ↩︎

